The phase portrait of a nonlinear pendulum.

DRAFT VERSION: Using this as an excuse to test the blog!

The motion of a nonlinear pendulum is governed by the well known equation,

\[\begin{align} \dfrac{d^2 x}{d t^2} + \sin x = 0 . \end{align}\]

The above equation is an example of a second-order, nonlinear ordinary differential equation (ODE). We can now introduce the following coordinate,

\[\begin{align} y & = \dfrac{d x}{d t}, \end{align}\]

and converted the second order ODE into a system to two first order ODEs, viz.,

\[\begin{align} \dot{x} & = y, \\ \dot{y} & = - \sin x. \end{align}\]

Here, dot denotes a derivative with respect to time.

We can now introduce a vector \(\vec{S} = x \hat{i} + y \hat{j},\)

and write our $2D$ system as,

\[\begin{align} \dfrac{d \vec{S}}{d t} = \begin{bmatrix} S_2 \\ -\sin S_1 \end{bmatrix}= \begin{bmatrix} y \\ -\sin x \end{bmatrix}, \end{align}\]

where $S_i$ is the $i$-th component of $\vec{S}$.

Our task is to analyse the behaviour of this system, and we do that by

• drawing the phase portrait of the system,
• solving the system of ODEs numerically.

We shall use python to perfrom the above tasks. We begin by importing suitable python libraries,

• numpy to perform manipulations over numeric arrays
• scipy.integrate.solve_ivp to numerically solve our ODEs
• matplotlib to plot the results
• seaborn to make the graphs look pretty.

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
import seaborn as sns
sns
.set_style("darkgrid")

Our first task is to code up a function that returns the right hand side (RHS) of the system.

def f(S, t=0):
    x, y = S
    return [y, -np.sin(x)]

Notice that

• our function takes two arguments $S$ and $t$.
• although our system is autonomous (that is, the RHS is independent of time), we still include the independent variable, this is because our ODE solvers are designed to accept functions which depend on both the variables.
  • the order of the arguments in the function signature is important, solve_ivp expects the independent variable first.
  • moreover, we set $t$ to take a default value $(0)$, so that can avoid passing a superficial argument while plotting the functions; we keep the $t$ to ensure we can use the same function for numerically solving the ODEs and for plotting the phase portrait.

Our first order of business is to generate the phase portrait: we have to essentially sketch the vector field

\[\begin{align} \dot{\vec{S}} & = \dot{x} ~ \hat{i} ~ + ~ \dot{y} ~ \hat{j},\\ & = y ~ \hat{i} ~ - ~ \sin x \hat{j}. \end{align}\]

To plot a vector field, we need the following two functions:

• numpy.meshgrid to generate a grid of points (over the 2D plane) where we must calculate the value of the components of the vector field.
• matplotlib.pyplt.streamplot to visualize a vector field by plotting the streamlines of the vector flow.

fig, ax = plt.subplots(figsize=(40,10))

xmin, xmax = -4.0*np.pi, 4.0*np.pi
ymin, ymax = -3.0, 3.0

x = np.linspace(xmin, xmax, 30)
y = np.linspace(ymin, ymax, 30)

XX , YY = np.meshgrid(x, y)

xdot, ydot = f([XX, YY])

ax.streamplot(XX, YY, xdot, ydot, density = 2)

plt.show()

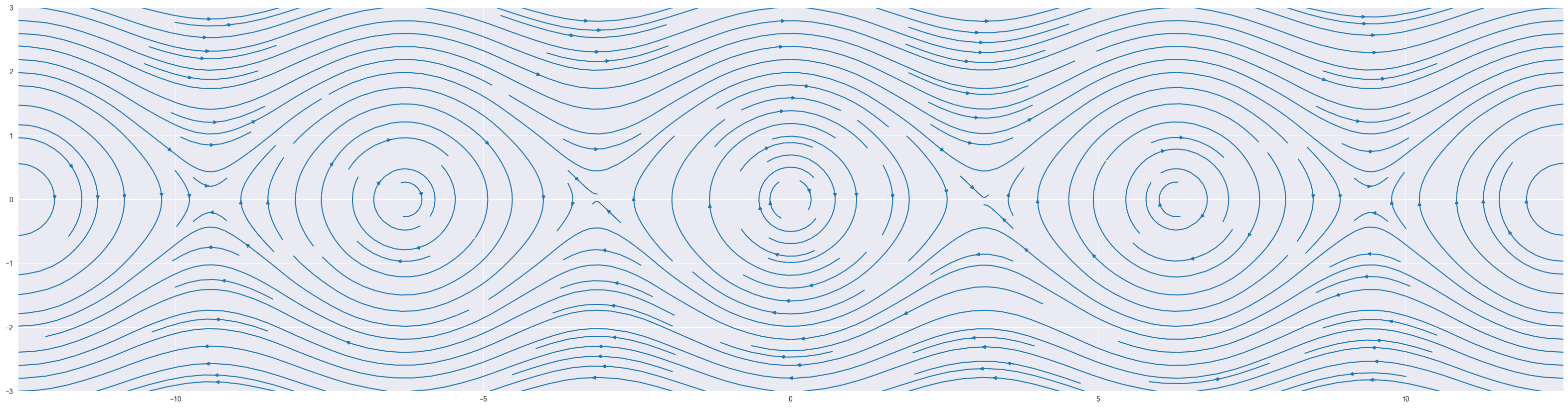
In the above code block, we,

• first set up the figure and axes object (if this looks unfamiliar, check this out
• we then set appropriate ranges for the variables, $x$ and $y$.
• we use numpy.linspace to generate 30 points along the $x$ and $y$ axes each.
• we then use numpy.meshgrid to obtain two 2D arrays $XX$ and $YY$ that helps us in computing the vector field over the entire $x-y$ plane.
• we store the values of the components of the vector field in xdot and ydot.
• finally we use matplotlib.pyplot.streamplot to sketch the vector field.

The primary purpose of using meshgrid is to avoid using slow python loops. To get a better understanding of how meshgrid works, check this out.

Notice the line where streamplot is invoked. The basic syntax is:

ax.streamplot(x_grid,y_grid,x_vec,y_vec, density=spacing)

Here x_grid and y_grid are arrays of x, y points. The arrays x_vec and y_vec denote the stream velocity at each point on the grid. The keyword argument density=spacing specifies how close the streamlines are drawn together.

We shall now use odeint to numerically solve the $2D$ system.

Since, we have two differntial equations, we have to provide two initial conditions. First, shall try to simulate the case where the bob of the pendulum is initially at rest, and it is set into motion with some initial velocity, that is,

\(x(0) = 0, ~ y(0) = c,\) where $c$ is a constant.

fig, ax = plt.subplots(figsize=(40,10))

t0, tf = 0.0, 45.0
tspan = np.linspace(t0, tf, 1000)

x0 = 0.0

c = np.linspace(-2.0, 2.0, 10)

for y0 in c:
    S0 = [x0, y0]
    ys = odeint(f, S0, tspan)
    ax.plot(ys[:,0] , ys[:,1], 'r-')

plt.show()

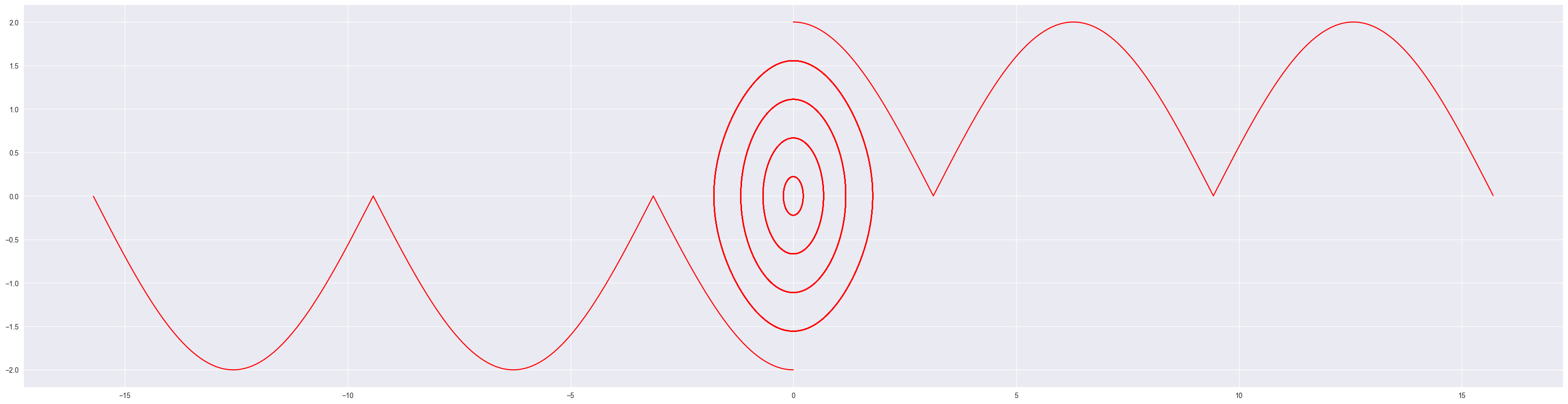
In the above code block, we:

• first set up the figure and axes object
• set up the time interval over which we solve our ODEs
• provide the first initial condition, $x(0)=0$
• we then construct an array containing suitable values of $c$ which we shall use to provide the second initial condition
• we then run a loop that picks up one element after the other from the array containg $c$ and calls the ODE solver with the initial conditions $[0,c]$
• the solution is stored in ys and then plotted.

We have used odeint to solve our ODEs; the syntax is ys= odeint(model, initial_values, t) where

• model is the RHS of the 2D system
• initial values is an array containing the initial conditions
• t is an array containing the point on the time axis where the ODEs are solved

odeint returns a matrix which has $k$ columns, one for each of the $k$ variables, and a row for each time point specified in t.

Lastly, I will change some attributes of seaborn to change the colour of the plots and define a helper function to plot arrows along the trajectories on the phase space. The detailed working of this function is not important.

#define seaborn background colors
sns.set(rc={'axes.facecolor': '#252a34','figure.facecolor':'#252a34'})

def plotarrows(xs, ys):
    s = int((xs.size)/100)
    xs = xs.reshape(-1,s)[:,1:].flatten()
    ys = ys.reshape(-1,s)[:,1:].flatten()

    for i in range(0, xs.size, 2):
        dx = xs[i+1] - xs[i]
        dy = ys[i+1] - ys[i]
        ax.arrow(xs[i], ys[i], dx, dy,
                  shape='full', lw=0, length_includes_head=True, head_width=.06, color='#ee5f5b')

We now put everything together.

• we sketch the vector field field (that is, draw the phase portrait)
• we solve the ODEs with the initial conditions
  • $x(0)= 5 \pi, y(0)= c ~ \mathrm{where} ~ c \in [-2, -1]$
  • $x(0)= -5 \pi, y(0)= c ~ \mathrm{where} ~ c \in [1, 2]$
  • $x(0)= 0 \pi, y(0)= c ~ \mathrm{where} ~ c \in (-2, 2)$
  • and then plot everything

fig, ax = plt.subplots(figsize=(40,10))

xmin, xmax = -4.0*np.pi, 4.0*np.pi
ymin, ymax = -3.0, 3.0

x = np.linspace(xmin, xmax, 30)
y = np.linspace(ymin, ymax, 30)

XX , YY = np.meshgrid(x, y)

xdot, ydot = f([XX, YY])

ax.streamplot(XX, YY, xdot, ydot, density = 2, color='#52adc8')


t0, tf = 0.0, 45.0
tspan = np.linspace(t0, tf, 1000)

x0 = 5.0*np.pi
c = np.linspace(-2.0, -1.0, 4)

for y0 in c:
    S0 = [x0, y0]
    ys = odeint(f, S0, tspan)
    ax.plot(ys[:,0] , ys[:,1], color='#ee5f5b')
    plotarrows(ys[:,0],ys[:,1])

x0 = -5.0*np.pi
c = np.linspace(1.0, 2.0, 4)



for y0 in c:
    S0 = [x0, y0]
    ys = odeint(f, S0, tspan)
    ax.plot(ys[:,0] , ys[:,1], color='#ee5f5b')
    plotarrows(ys[:,0],ys[:,1])

x0 = 0
c = np.linspace(-1.95, 1.95, 10)

tspan = np.linspace(t0, tf, 300)

for y0 in c:
    S0 = [x0, y0]
    ys = odeint(f, S0, tspan)
    ax.plot(ys[:,0] , ys[:,1], color='#ee5f5b')
    plotarrows(ys[:,0],ys[:,1])

ax.set_xlim(xmin, xmax)
ax.set_ylim(ymin, ymax)

# uncomment for grid lines but no labels
# ax.set(yticklabels=[]) # hide y labels
# ax.set(xticklabels=[]) # hide x labels

plt.axis('off')

plt.show()
fig.savefig("header.png", dpi=300)

References:

[1] Nonlinear Dynamics and Chaos, 2nd Ed by Steven Strogatz, CRC Press (2015).